سوف نوضح لكم طريقة الأعداد الكسرية، تمثل أجزاء أو أقسام من قيمة محددة، وتكتب على شكل كسر يتألف من بسط ومقام (أ/ب)، والبسط يمثل الجزء العلوي من الكسر، بينما يمثل المقام الجزء السفلي، وكلاهما أعداد صحيحة، ولا يمكن للمقام أن يكون صفراً، ويمكن كتابة الأعداد الكسرية أيضًا كأعداد مختلطة، حيث يوضع العدد الصحيح بجانب الكسر.
جدول المحتويات
ماهي الأعداد الكسرية
هي الأعداد التي تمثل جزءًا من العدد الكلي، وتتكون من بسط ومقام، حيث يمثل البسط الجزء العلوي من الكسر والمقام الجزء السفلي، ويكتب على شكل كسر (أ/ب)، حيث “أ” هو البسط و”ب” هو المقام، على سبيل المثال، ٣/٤ هو كسر يمثل ثلاثة أرباع، وإلى جانب تمثيل الجزء المقسم من العدد الكلي، يمكن استخدام الأعداد الكسرية في العديد من السياقات مثل الرياضيات والعلوم والاقتصاد والهندسة وغيرها، على سبيل المثال، في الرياضيات، يستخدم الكسور لتمثيل النسب والتقديرات الكمية التي لا تكون عددًا صحيحًا، وفي العلوم، يستخدم الكسور لتمثيل النسبة المئوية والتجارب العلمية، وفي الهندسة، يستخدم الكسور لتمثيل الأبعاد والنسب الهندسية.

طريقة ضرب الأعداد
تمثيل أيضاً على شكل كسر مختلط، حيث يتكون من بسط ومقام وعدد صحيح، ويتم وضع العدد الصحيح بجانب الكسر، وفيما يلي توضيح لخطوات ضرب الأعداد الكسرية؛
- يتم ضرب بسط العددين الكسريين معا ومقام العددين الكسريين معًا للحصول على الكسر الناتج.
- يتم وضع البسط الناتج فوق المقام الناتج.
- إذا كان الكسر كبيرًا، يمكن تبسيطه عن طريق قسمة البسط والمقام على أكبر مشترك بينهما.
ولضرب عدد كسري × عدد كسري مختلط، يمكن اتباع الخطوات التالية:
- يتم تحويل العدد الكسري المختلط إلى عدد كسري عادي.
- بالتالي يضرب العدد الصحيح في مقام الكسر ويجمع الناتج مع بسط الكسر.
- ثم يوضع المجموع كبسط جديد على مقام الكسر الأصلي.
- بعد ذلك يضرب البسط في البسط ويضرب المقام في المقام للعددين الكسريين.
- يتم وضع البسط الجديد فوق المقام الجديد، ثم يبسط الناتج للحصول على أبسط صورة.
استخدامات الأعداد الكسرية
الأعداد الكسرية لها العديد من الاستخدامات في مختلف المجالات،ونعرض بعض الاستخدامات الشائعة، ويظل هناك العديد من الاستخدامات الأخرى في مجالات متعددة، بما في ذلك:
اقرأ أيضًا: تهنئة اليوم الوطني العراقي
- الرياضيات تستخدم في حسابات النسب والتقديرات الكمية التي لا تكون عددًا صحيحًا، وفي الجبر لحل المعادلات وتبسيط التعابير.
- العلوم تستخدم في حساب النسب المئوية، وفي تمثيل النتائج العلمية والقياسات الدقيقة.
- الاقتصاد تستخدم في حساب النسب المئوية للزيادات والنقصانات، وفي تحليل البيانات المالية والاقتصادية.
- الهندسة تستخدم في تمثيل الأبعاد والنسب الهندسية في المخططات والرسومات الهندسية.
- الطهي والخبز في بعض الوصفات، يستخدم الكسر لتحديد كميات المكونات بدقة.
- الرياضات والألعاب الإلكترونية يستخدم الكسر في حساب نقاط وتقييم أداء اللاعبين.
- المالية الشخصية حيث تستخدم الكسور في حساب الميزانية الشخصية وتوزيع النفقات.
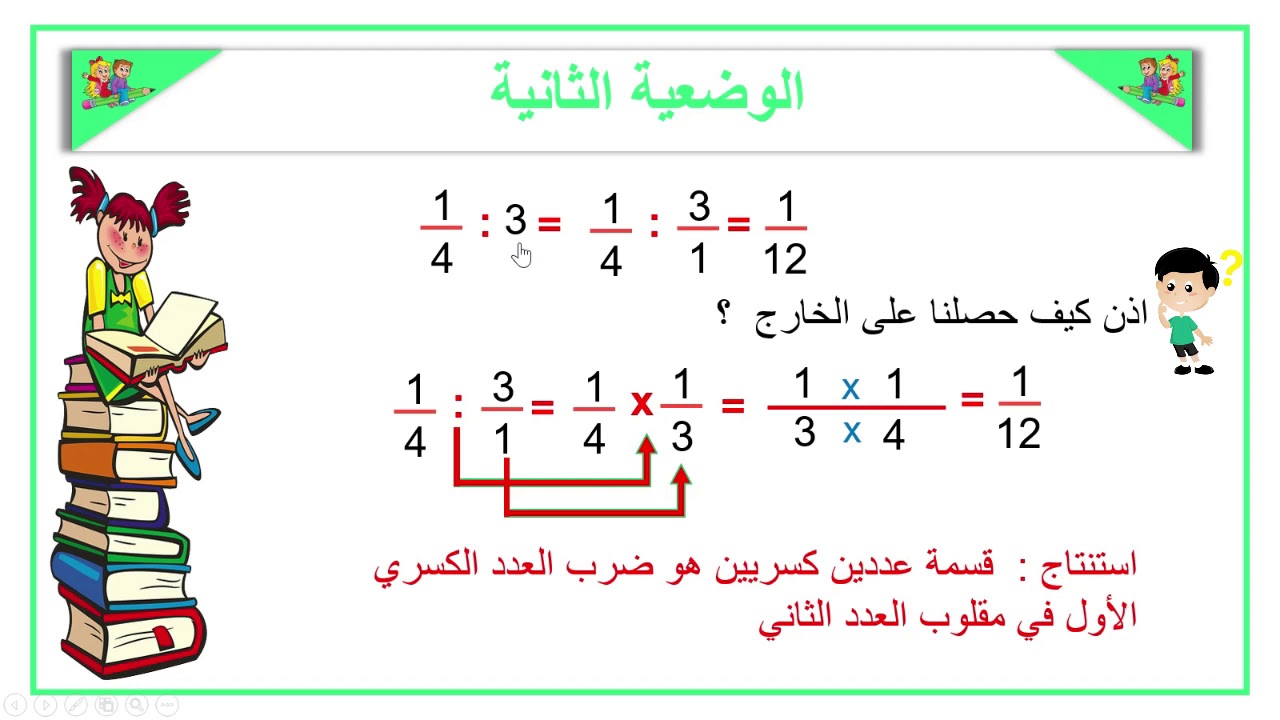
طريقة قسمة الأعداد الكسرية
توضح مجموعة الخطوات التالية الطريقة الصحيحة لكيفية قسمة الأعداد الكسرية، وهي كالتالي:
- البقاء على العدد الكسري الأول كما هو.
- استبدال عملية القسمة بعملية الضرب.
- عكس العدد الكسري الثاني بقلبه وجعل البسط مقاما والمقام بسيطا.
- ضرب العددين الكسريين باتباع الخطوات التالية؛ ضرب البسطين، ثم ضرب المقامين، ثم تبسيط الناتج للحصول على أبسط صورة.
- في حال وجود عدد كسري مختلط، يتم تحويله إلى عدد كسري عادي، ثم يتم استئناف عملية الضرب.
جمع الأعداد الكسرية
عند جمع الأعداد الكسرية، يتغير الطريقة اعتمادا على ما إذا كانت مقامات الكسور متحدة أم لا؛
- في حال كانت متحدة، يمكن جمع الكسور مباشرة عن طريق جمع البسط مع الحفاظ على المقام، أما إذا كان البسط أكبر من المقام، يتم تحويل الناتج إلى عدد كسري وإضافة الجزء الصحيح إلى العدد الصحيح الأصلي، ويتم كتابة الناتج كعدد كسري مختلط.
- في حالة عدم توحيد المقامات، يجب توحيدها قبل البدء في الجمع، يتم ذلك عن طريق البحث عن العامل المشترك الأصغر (LCM) للمقامات المختلفة، وبعد توحيد المقامات يتم جمع الكسور مباشرة عن طريق ضرب كل من البسط والمقام في الكسر الذي يحتوي على المقام الأصغر بالعامل المشترك الأصغر، وبعد الجمع يتم التحويل إلى عدد كسري إذا كان البسط أكبر من المقام، ويضاف الجزء الصحيح الناتج من التحويل إلى العدد الصحيح الأصلي، ثم يتم كتابة الناتج مع العدد الصحيح الكلي إلى جانب الكسر.
اقرأ أيضًا: الرد على حصل خير بالعامية
باختصار فإن الأعداد الكسرية تشكل جزءًا أساسيا من الرياضيات والعديد من المجالات الأخرى، وتعتبر طريقة دقيقة لتمثيل الأجزاء من الكميات الكلية وتسهم في حل المسائل وتطبيقات الحياة اليومية، ومن خلال فهمنا للأعداد الكسرية، نستطيع توظيفها بفعالية في حل مشاكل متنوعة وفهم العلاقات الرياضية بشكل أفضل.