سوف نقدم لكم الان بحث عن الاشكال الرباعية، الأشكال الرباعية هي جزء أساسي من الهندسة الهندسية، حيث تتميز بتكوينها من أربعة أضلاع، وتمثل هذه الأشكال جزءا أساسيا من تصميماتنا وتشكيلاتنا اليومية، ويمتلك كل شكل رباعي خصائصه الفريدة وزواياه المميزة، وفي هذا النص، سنستكشف مفهوم الأشكال الرباعية، وأنواعها المختلفة، بالإضافة إلى خصائصها التي تميزها وتجعلها جزءًا لا يتجزأ من دراسة الهندسة والرياضيات.
جدول المحتويات
كيفية البحث عن الاشكال الرباعية
- الأشكال الرباعية والمجسمات تمثل جزءًا أساسياً من مبادئ علم الهندسة، حيث تشكل جزءًا من تصنيفات الأشكال الهندسية.
- وتتألف كل مجسم من أربعة أضلاع، ويعرف هذا النوع من الأشكال بالمضلع.
- وتعرف المحيط في كل الأشكال الهندسية بمجموع أطوال الأضلاع الأربعة.
- تتنوع الأشكال الرباعية الهندسية في أنواعها، حيث تشمل المتوازي المستطيلات والمربعات والمعينات والمستطيلات والأشكال ذات الأضلاع المنحرفة.
- ولكل نوع من هذه الأشكال خصائصه الفريدة التي تميزه عن الآخر، بالإضافة إلى وجود أساليب مختلفة لحساب كل من مساحتها ومحيطها.
- بالإضافة إلى الأشكال الرباعية، هناك أشكال هندسية أخرى غير رباعية الأضلاع مثل المثلثات والدوائر والأشكال ثنائية الأبعاد.
- ولكل نوع من هذه الأشكال خصائصه وتفاصيله التي تميزه عن الباقي، وتسهم في فهم تصميمه واستخدامه في مجالات مختلفة.
تعريف الأشكال الرباعية وأهم خصائصها
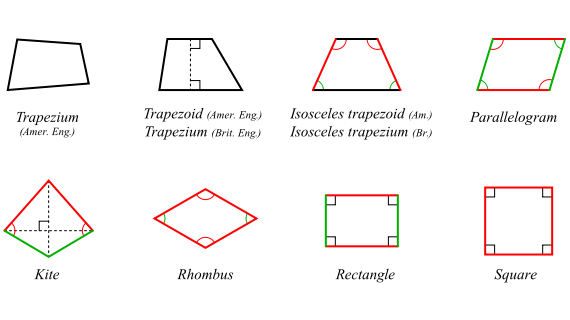
- تعتبر الأشكال الرباعية جزءا أساسيا من مجال الهندسة الذي يستمد من مبادئ الرياضيات، ويعتبر الشكل الرباعي كل هيكل يحتوي على أربعة أضلاع أو جوانب. وتتميز هذه الأشكال بوجود أربعة زوايا وأربعة أطراف، حيث اشتق اسمها من عدد الأضلاع التي تتكون منها.
- تتنوع الأشكال الرباعية في أشكالها وأنواعها، بما في ذلك المتوازي المستطيلات والمعين والمربع والمستطيل.
- وبشكل عام فإن فهم الأشكال الرباعية يساعد في فهم العديد من المفاهيم الهندسية الأساسية والتطبيقات العملية في الحياة اليومية والعلمية.
اقرأ أيضًا: مقدمة عن اليوم العالمي للتطوع
خصائص الأشكال الرباعية بشكل عام
- يتألف الشكل الرباعي من أربعة أضلاع أو زوايا أو جوانب أو رؤوس.
- الضلعان المتقابلان في الشكل الرباعي لا يشتركان في ضلع مشترك.
- الرأسين المتقابلين لا ينتميان إلى نفس الضلع في الشكل الرباعي.
- الرأسان المتقابلان هما زاويتان يقابلان في الشكل الرباعي.
- القطر الكامل للشكل الرباعي يكون داخل المضلع.
- قطع الشكل الرباعي يكون كاملاً خارج المضلع.
- مجموع قياسات زوايا الشكل الرباعي يساوي 360 درجة.
- جميع الأشكال الرباعية هي ثنائية الأبعاد دون أي استثناء.
اقرأ أيضًا:اذاعة مدرسية عن حقوق الطفل
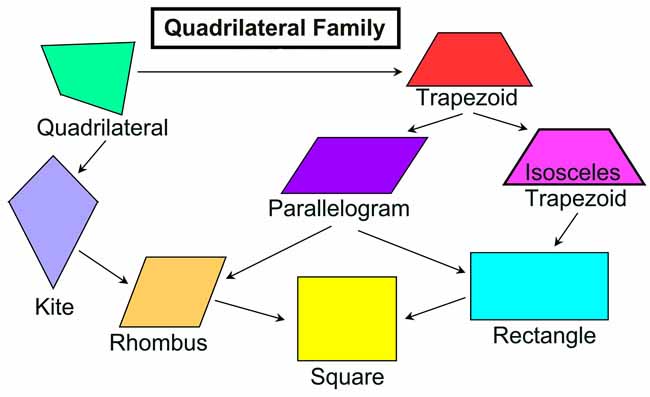
أنواع الأشكال الرباعية والمجسمات
متوازي الأضلاع:
- يشكل متوازي الأضلاع شكلا مسطحة ومغلقا مع أضلاع متوازية.
- الأضلاع المتقابلة ذات طول متساو.
- يتكون من أربع زوايا، وكل زوج من الزوايا المتقابلة متساو في القياس.
المربع:
- جميع الأضلاع في المربع متساوية في الطول.
- تتساوى زواياه الأربع في 90 درجة.
المعين:
- أضلاعه المتقابلة متوازية في الطول.
- زواياه متساوية في القياس.
المستطيل:
- كل زاوية في المستطيل تقدر بـ 90 درجة.
- أضلاعه المتقابلة متساوية في الطول.
شبه المنحرف:
- يتميز بأن لديه زوايا قائمة.
- الأضلاع المتقابلة متساوية في الطول.
- يتكون من قاعدتين وارتفاعٍ عمودي بينهما، وضلعين آخرين غير متساويين.
خصائص الأشكال الرباعية
خصائص الأشكال الرباعية تتنوع وتتميز كل نوع بميزاته الفريدة والتي تحدد مساحته ومحيطه، وفيما يلي نستعرض خصائص كل منها:
المربع:
- شكل رباعي منتظم، حيث تكون جميع زواياه قائمة.
- القطران متساويان ومتعامدان.
- مساحته يتم حسابها بضرب طول الضلع في نفسه.
- محيطه يتم حسابه بضرب طول الضلع في عدد الأضلاع.
المستطيل:
- جميع الضلعين المتقابلين متوازيان ومتساويان في الطول.
- لديه محور تماثل وقطر يقسمه إلى مثلثين.
- مساحته يتم حسابها بضرب الطول في العرض.
- محيطه يتم حسابه بجمع الطول والعرض وضرب الناتج في 2.
- المعين:
- جميع الأضلاع متساوية في الطول والزوايا.
- مساحته يتم حسابها بنصف حاصل ضرب القطرين.
- محيطه يتم حسابه بضرب طول الضلع في 4.
متوازي الأضلاع:
- كل زاويتين متتاليتين يساويان 180 درجة.
- مساحته يتم حسابها بضرب القاعدة في الارتفاع.
- محيطه يتم حسابه بجمع أطوال الأضلاع.